
|
My Projects Courses Writings
Source Code Social Networks |
Main /
Les nombres universVers l'Infini et au delàLa constante de Champernowne, un simple nombre... universLe dernier nombre que je viens de faire rentrer dans la famille de Decimals Search est la constante de Champernowne en base 10 C(10). Les décimales de cette constante sont facilement calculables pour n'importe quelle personne sachant compter. En effet, David Gawen Champernowne, statisticien renommé du Royaume-Uni, a démontré qu'en concaténant les entiers naturels positifs les uns à la suite des autres pour en former les décimales, nous obtenons un nombre transcendant parfaitement normal et donc univers ! L'ensemble des entiers naturels positifs sont donc dans les décimales de cette constante et nous savons tous que cet ensemble est infiniment grand. Vous pouvez donc prendre n'importe quelle suite de chiffres, aussi grande que vous le souhaitez, elle sera de toute évidence présente dans les décimales de C(10) et une infinité de fois en plus. Prenons la suite '11' par exemple : on la retrouve dans le nombre 11, dans le nombre 110, dans le nombre 111, dans le nombre 211... etc. J'appelle cela des similarités. La suite '11' est ainsi présente une infinité de fois dans l'ensemble infini des entiers positifs et donc dans les décimales de C(10). Et cela fonctionne pour n'importe quelle autre suite. Toutes les décimales de C(10) Toutes les décimales de C(10) en caractères ASCII
Techniquement, le calcul des décimales de C(10) ainsi que des similarités est effectué côté client. C'est à dire que c'est directement votre appareil (ordinateur, tablette ou smartphone) qui calcule contrairement aux autres nombres irrationnels comme Pi, racine de 2, phi... où c'est le serveur qui fournit les décimales. Afin de travailler avec de très très grand nombres qui dépassent largement la taille maximale d'un double sur une architecture 64 bits, j'ai utilisé une librairie JavaScript (BN.js pour BigNumber.js) développé par Fedor Indutny. Cette librairie représente les nombres dans des structures de données type liste de tableaux. Les mathématiques, le code de Dieu ?J'adore les mathématiques mais je ne suis pas très bon. Je suis fasciné par les nombres univers. Dans leur infinité de décimales, vous avez mot pour mot tout le contenu du dernier livre que vous avez acheté. C'est juste incroyable. Votre code génétique tout entier, vos photos de vacances (mêmes ratés, mêmes photoshopés), votre passé, votre futur, les plans de construction du prochain Airbus, les Gold Codes générés quotidiennement par la NSA, les combinaisons gagnantes et perdantes du loto, toutes les vidéos plan par plan, les musiques, ce que je suis en train d'écrire... tout cela est quelque part dans les décimales... Quoiqu'il puisse y avoir dans le temps, ABSOLUMENT TOUT n'est qu'un extrait déjà écrit depuis toujours dans leurs décimales. Il y a juste que c'est dans le désordre et donc totalement inexploitable. 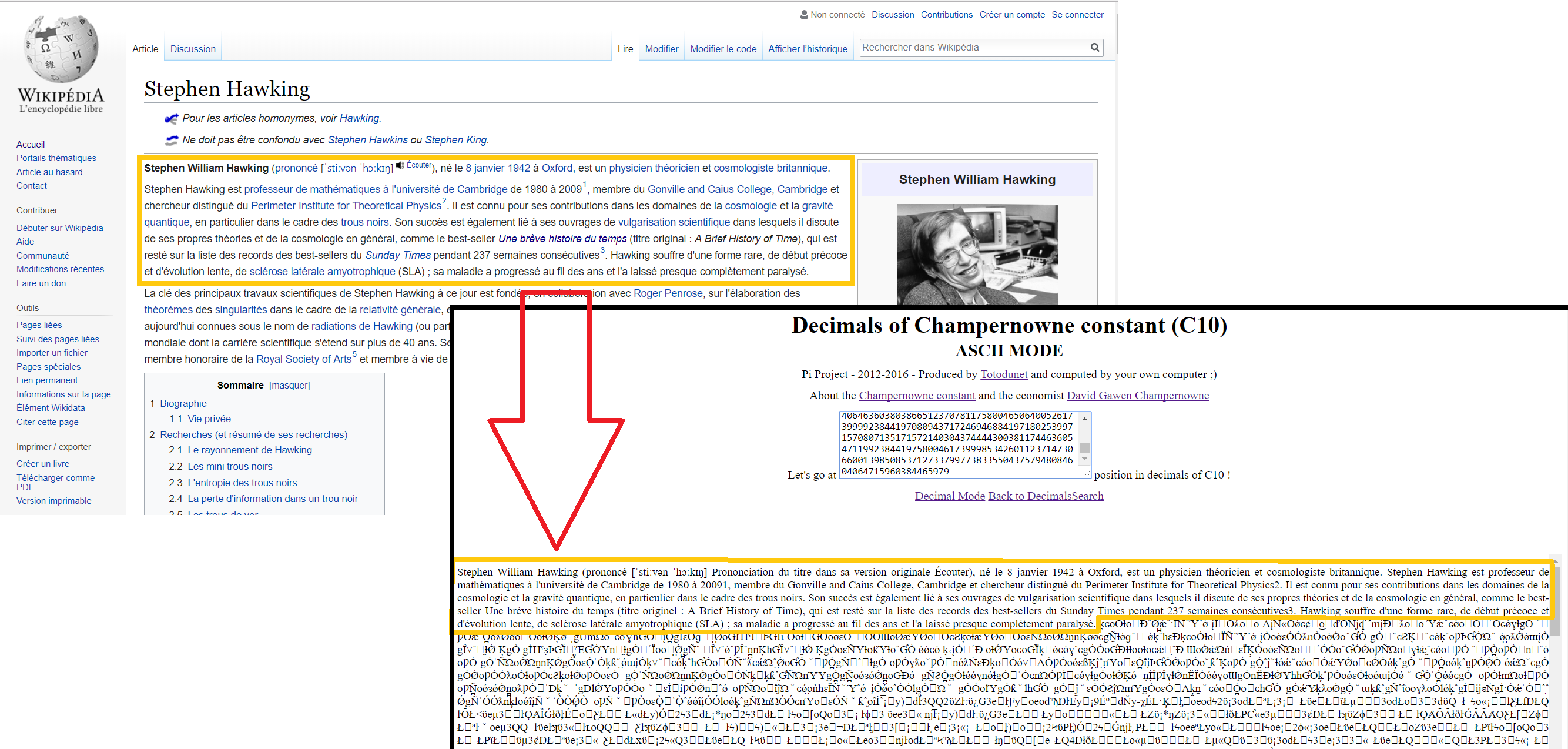 Le premier paragraphe de la page Wikipédia de Stephen Hawking a été retrouvé à cette position dans les décimales de la constante de Champernowne en base 10. Il ne s'agit bien entendu que d'une similarité parmi une infinité. La personne qui voudrait s'approprier le contenu illimité de cette page, bien que ce soit impossible, pourrait se trouver être la personne la plus puissante de l'Univers. En effet, elle pourra se voir posséder le Tout et revendiquer ainsi toute future production ou future découverte comme sa propriété. Car on sait forcément que quoi qu'il puisse y avoir, c'est de toute évidence déjà écrit dans les décimales de C(10) ou de tout autre nombre univers. Champernowne a de la veine d'avoir un tel nombre qui porte son nom. Pour rigoler je dis souvent à mes collègues : "Si Pi est univers, alors toutes les solutions à tous nos problèmes solubles se trouvent simplement dans ses décimales. Sinon c'est dans la constante de Champernowne. Il suffit de chercher." Je vous invite à regarder du côté des histoires de la bibliothèque de Babel et du singe savant qui illustrent très bien l'Infini. L'Univers ou l'Infini ?Mais finalement la constante de Champernowne n'est juste qu'un nombre parmi l'infinité des nombres réels. Et si on affirme que tout est contenu dans les décimales de C(10), alors cela voudrait dire que tout le contenu infini de la page Web plus haut est quelque part lui aussi dans cette même page Web ? C'est paradoxal mais c'est précisément là où je suis fasciné, on peut supposer des infinis dans des infinis. Par exemple, on est d'accord que les décimales de Pi sont infinies. Et je peux vous assurer que toutes ses décimales sont contenues dans les décimales de C(10) mais il m'est impossible de donner une position. Par contre si on ne se limite qu'aux 20 premières décimales de Pi, on a une similarité à la 272.074.196.068.475.365.810ème position. Pour les 30 premières, on en retrouve une à la 4.136.668.496.582.686.042.768.190.387.260ème position et c'est vrai pour autant de décimales de Pi que vous le souhaitez soit l'infini donc. Et ce qui est rigolo dans tout ça, c'est que si Pi serait univers (mon fantasme), alors on retrouverait l'infinité de décimales de C(10) dans Pi une infinité de fois alors que l'on vient de voir que ce dernier présente déjà lui même une infinité de similarités dans C(10). Enfin au moins, avec le même raisonnement que l'on vient d'avoir, on est certain que l'infinité des décimales de C(10) est compris une infinité de fois dans C(10) lui même... Ça fait mal à la tête certes mais c'est incroyable ! 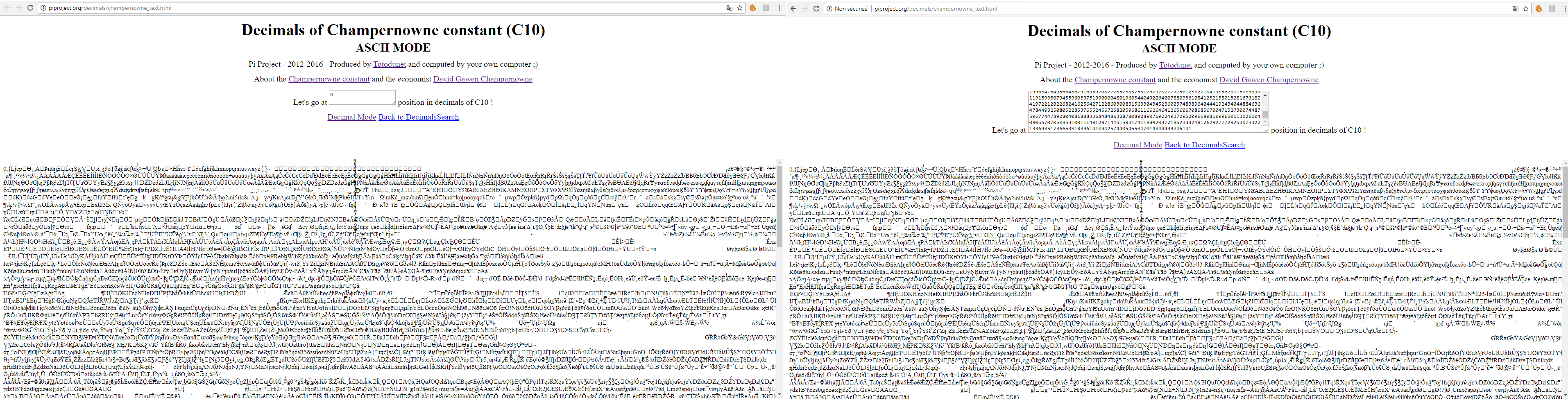 On retrouve caractère pour caractère le début de la page dans elle même. A gauche, la position 0 et à droite cette position. Si on prend l'histoire de la bibliothèque de Babel qui comprend un nombre infini de livres, ces derniers contiennent tous 1312000 caractères précisément (410 pages de 40 lignes de 80 caractères). Il y a 25 caractères différents, on comptabilise donc 25^(1312000) livres distincts. Et l'infinité des ouvrages restants de la bibliothèque ne sont que de simples copies. Maintenant si je décide de leur rajouter à tout les livres de la bibliothèque 1 caractère de plus, le nombre de combinaisons possibles change. On a alors 25^(1312001) livres distincts. Ou encore mieux si je décide à la place d'étendre l'alphabet d'un nouveau caractère supplémentaire, on compte désormais 26^(1312000) livres distincts. Selon comment l'information est découpée, le nombre de combinaisons distinctes variera mais ces combinaisons ne ferons que se répéter quand même. En écrivant ces lignes, cela me rappelle tout juste d'un projet perso de plugin jQuery que j'ai développé il y a quelques années, en 2014 je crois, Endless.js. L'idée est de pouvoir avoir du contenu qui se répète indéfiniment. Un artiste et philosophe à la fois a d'ailleurs utilisé le plugin pour une de ses œuvres. ConclusionPS: Les extraits des films ne contiennent pas de spoils (sauf peut-être la deuxième vidéo mais ce n'est pas la fin, il n'y a pas vraiment de chute). Vous pouvez donc les visionner même si vous n'avez pas vu les films. Il n'y a aucun problème. Je vous conseille ensuite de les regarder car ils sont très beaux.Si notre Univers a les mêmes propriétés mathématiques qu'un nombre univers, ce n'est alors qu'un puits sans fond d'information qui se répète non périodiquement sans cesse. Il est presque évident que, perdu dans cet étendu immensurable, il y ait des copies "parfaites" de tout à un instant T, car infini et non ultimement périodique. Il n'est donc vraiment pas déconnant de penser qu'il y ait des clones de nous, qui nous ressemblent, qu'ils aient les mêmes activités et qui vivent en ce moment quelque part dans de "très lointaines" galaxies. Des vies parallèles... Mais les similarités que l'on trouvera avec eux dépendront de la quantité d'information qui a été utilisée pour nous coder. Nous sommes par contre, si il y a un infiniment petit, des quantités infinies d'informations dans le grand Infini. Prenons les atomes par exemple, on a pensé qu'ils étaient tous pareil et que c'était les plus petites particules à constituer la matière et on en dénombre une infinité... Mais si on approfondit et que l'on va un peu plus loin vers l'infiniment petit, on voit que les atomes sont constitués eux mêmes de neutrons et de protons en nombre différents. On a tout simplement changé la façon de décrire les choses et intégrer plus d'information. On a, comme pour les livres de la bibliothèque de Babel, augmenter le nombre de combinaisons possibles d'atomes distincts. Et le nombre est d'autant plus grand si on va encore plus loin dans la description et que l'on commence à s'occuper en détail de ses constituants. Et ainsi de suite vers l'infiniment petit. Mais malgré tout les détails inimaginables que l'on pourrait rajouter pour décrire les éléments, cette quantité d'information aussi grande soit-elle, ne peut jamais rivaliser avec le grand Infini et est toujours répétée indéfiniment.
Ce qui m'a toujours intrigué maintenant c'est comment pouvons-nous être une quantité infinie d'information dans le grand Infini ? Le fait de supposer des infinis dans l'Infini est assez étrange. Comment peut-on dire qu'un infini est plus petit que l'Infini si leur taille est incomparable (en terme de quantité je parle, pas d'intervalle) ? Autrement dit, si notre Univers est bien Infini comme on le dit, il n'y a pas de limites et ce n'est donc pas la peine de chercher à savoir où nous sommes et ce que nous représentons : nous sommes éternellement perdus. Nous sommes condamnés à explorer ce qu'il y a tout autour de nous, infiniment plus près, infiniment plus loin, dans une infinité de directions, et par dessus tout, en changement continu avec le Temps. Un travail d'Hercule interminable que même si on enlève la notion de temps, la tâche reste irréalisable. Ok ça devient philosophique mais ça explique pourquoi nous n'arrêterons jamais de faire de la Science... et que nous ne soyons jamais assez à en faire... Cette idée me fascine et me désespère à la fois. Fasciné par le fait qu'il y aura toujours des cadeaux qui s'offriront à nous et désespéré de savoir que nous ne puissions jamais tous les ouvrir. Nous nous apercevons qu'avec ce raisonnement, il n'y a finalement que du Rien dans ce Tout. Et le Tout n'est, face à lui même, que du Rien. C'est le paradoxe de l'Infini. Il n'y a rien de validé. J'ai juste écrit ce que je pensais. Comme vous avez pu le constater, je vois l'Univers avec mes yeux d'informaticien et je crois qu'il peut être représenté par un mot infini non ultimement périodique tel que l'infinité des décimales d'un nombre univers. Il y a d'autres façons de le percevoir. Vous pouvez donc ne pas être d'accord, me prendre pour un fou et considérer que ce que je vous ai raconté c'est du gros bullshit. Après tout l'Infini n'est qu'un concept. Nombreux sont ceux qui cherchent encore et encore une théorie du Tout, notamment l'éminent cosmologue Stephen Hawking qui tente toujours, par la physique théorique, de résumer l'Univers en une seule équation mathématique.
En attendant, que ce soit les scientifiques avec leurs théories, les philosophes avec leurs courants de pensées ou encore les religieux avec leurs contes, aucun n'a encore su apporter une preuve irréfutable sur le pourquoi il y a quelque chose plutôt que rien. Tout le monde est encore en train de rechercher Dieu dans l'histoire. Alors moi je leur dis de vive voix, bon courage et que celle ou celui qui aura la meilleure perception de l'Univers gagne ! Pour vous remercier d'avoir lu mon charabia jusqu'au bout, je vous montre ci-dessous une de mes scènes favorites (romantique en plus) du film "Un home d'exception". Je l'ai vu il y a quelques mois. On me l'a conseillé et je l'ai beaucoup aimé. C'est un biopic assez romancé du mathématicien américain John Nash. Je vous le conseille. Dans ce même genre de film que j'ai beaucoup aimé, il y a "Une merveilleuse histoire du temps..." qui est un biopic assez récent sur Stephen Hawking, où d'ailleurs la vidéo juste au dessus en est un extrait. Le film "Imitation Game", qui lui parle du cryptologue Alan Turing, est à voir également.
Le projet Pi et Decimals SearchA l'origine je voulais faire un site consacré seulement au nombre Pi. L'objectif du projet était de comprendre sa série infinie de décimales. Pi reste à ce jour un nombre mystérieux. On sait qu'il est irrationnel, que sa suite de décimales est infinie mais nous ne savons rien encore sur ses décimales même, s'il y a une période ou non par exemple. Bien que les premiers milliers milliards de décimales calculées montrent que Pi semble normal, et donc nous laissent penser qu'il serait un nombre univers, il n'y a aucune certitude. Il en est d'ailleurs de même pour le nombre racine de 2 qui pourrait nous cacher les mêmes propriétés. Et le calcul de ses décimales reste encore très coûteux en ressources (mémoire et unités de calcul) ce qui complique pas mal l'étude. Bien que maintenant les processeurs soient de plus en plus puissants. Le premier site du projet Pi est Decimals Search, un moteur de recherche de décimales de nombres irrationnels. Sorti en 2012, quelques temps après mon bac, des nombres irrationnels se sont rajoutés au fur et à mesure et j'ai essayé d'aller le plus loin possible dans le calcul des décimales. Ainsi au tout début, le site ne recensait que 1 milliard de décimales pour Pi. En 2016 il en recense au moins 53 milliards de décimales de Pi calculées par mes soins (enfin par ma machine) :
Plus récemment, 750 milliards de Pi sont disponibles sur Decimals Search depuis que Google s'est lancé dans la course début 2017 :
La première année, j'avais sorti aussi en parallèle un autre site, P.I.T., faisant lui aussi parti du projet Pi. C'était un solveur d'équations linéaires à 1, 2 et 3 inconnus ainsi que de matrices 3x3. Cela me permettait de vérifier mes résultats, voir carrément de faire mes exercices d'algèbre durant mes premières années de fac... Il n'existe plus aujourd'hui pour la bonne raison qu' à cette époque, j'écrivais mes sites en Visual Basic qui tournaient sur un serveur Microsoft IIS et que j'ai changé plus tard pour un serveur Linux. Financièrement, ce changement de serveur était beaucoup mieux pour moi bien que j'ai du recoder entièrement Decimals Search en PHP cette fois. Decimals Search a gagné en réactivité. Sauf que je n'ai en revanche pas pris la peine de refaire le solveur P.I.T. car j'en avais plus besoin. Je ne dis pas non pour le recommencer un jour maintenant que je ne trouve plus rien à faire sur Decimals Search. Cela fera un nouveau site pour le projet Pi. Mais j'ai aussi d'autres projets de dev. dans la tête qui ne sont pas forcément maths. Un petit mot sur la recherche actuelle de PiIl faut savoir qu'il y a des personnes, leur métier c'est d'étudier la constante Pi. Un chouette boulot. Ce sont principalement des mathématiciens et informaticiens. Parmi les personnes les plus connus dans ce domaine encore en activité :
Il y en a bien d'autres des chercheurs qui travaillent sur ce nombre et beaucoup d'amateurs également. Le record mondial du nombre de décimales de Pi calculées a été remporté le 21 novembre 2016 (1 mois après mon annonce dans une vidéo que j'arrêtais personnellement tout calcul des décimales après en avoir obtenu 53 milliards en 1.5 jour par mon PC) par Peter Trüb, ingénieur d'études chez Dectris, qui en a obtenu 22 400 milliards. Dectris est une société suisse qui fabrique des détecteurs optoélectroniques tel que des compteurs de photons. Le calcul, exécuté sur une très grosse machine, a duré 105 jours. L'intérêt d'avoir fait cela n'était pas vraiment pour Pi mais plutôt de mettre leur système de développement en mode stress full jusqu'à son plantage afin d'en connaître les limites de performance. En tout cas sur toutes les décimales calculées, Peter affirme que Pi semble normal. Il est possible de demander à Dectris les décimales calculées. Elles sont disponibles gratuitement. Vous pouvez même leur envoyer vos disques durs par la poste et ils vous les copient. Par contre il faudra prévoir 10TB d'espace disque. C'est pourquoi je ne peux évidemment pas me permettre de stocker autant de décimales de Pi sur Decimals Search, la capacité de stockage de mon serveur n'étant pas suffisante. Mais sinon vous pouvez leur demander une rangée spécifique de décimales. Article Avec la puissance des ordinateurs qui ne fait qu'augmenter, on en calculera toujours plus des décimales de Pi. Mais l'objectif ultime étant de trouver une formule simple qui permet d'obtenir n'importe quelle décimale et de savoir si, comme la constante de Champernowne, l'Univers est écrit dans Pi. |